LeetCode (Algorithms#5) ‒ Longest Palindromic Substring

Problem

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

Examples:

Given "cababade", return "ababa"
Given "gcaack", return "caac"

Solution

This problem is similar to that of the Longest Common Subsequence, and as most should suspect, can be solved using dynamic programming. Because we must consider all possible substrings as a palindrome, we can expect an (n)(n+1)/2=O(n^2) solution. There are quite a few ways to solve this in O(n^2), but the basic idea is that we keep track of all palindromes starting at i, and ending at j. When i==j and the characters at position i and j are equal, the character is a palindrome with itself of length 1. If the characters are equal and i!=j, then either the two same characters are next to each other, or are the beginning and end of a previous palindrome. In both cases we add 2 to account for the length of the character on both ends.

Below is the code for this approach. The loops run from the end of the string to produce a matrix A with the upper triangle containing lengths of palindromes. The maximum palindrome is kept track of and returned.

Time complexity: O(n^2)
Space complexity: O(n^2)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

public String longestPalindrome(String s) { int maxi = -1, maxj = -1, maxPal = 0, len = s.length(); int[][] A = new int[len][len]; for (int i = len - 1; i >= 0; i--) { for (int j = i; j < len; j++) { if (s.charAt(i) == s.charAt(j)) { if (i == j) A[i][j] = 1; else if (i+1 > j-1 || A[i+1][j-1] > 0) A[i][j] = A[i+1][j-1] + 2; if (A[i][j] > maxPal) { maxPal = A[i][j]; maxi = i; maxj = j; } } else { A[i][j] = 0; } } } return s.substring(maxi,maxj+1); }

LeetCode (Algorithms#4) ‒ Median of Two Sorted Arrays

Problem

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log(m+n)).

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

Solution

The idea behind this problem is quite simple. To find the median in O(log(n+m)), we need to perform some kind of binary search concurrently on both arrays. The difficulty is in making sure to consider all possible cases. Overall, there is a general case that performs the binary search, and a base case to chose the median among four or less remaining elements. The code below has the different cases commented. The idea is to keep track of how many elements have been removed from each side, and repeatedly split either array in half such that we remove the smaller or larger elements from the left or right side, respectively.

This is certainly not the most clean or efficient solution to this problem as there are many cases that need to be explicitly handled. Another solution is to use a recursive divide and conquer approach where you determine the two array's medians, and then recurse on the halves of the arrays that bring the medians closer (or equal to each other).

Time complexity: O(n+m)
Space complexity: O(n^2)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86

public double findMedianSortedArrays(int[] nums1, int[] nums2) { int len1 = nums1.length, len2 = nums2.length, len = len1 + len2; boolean evenlen = (len1 + len2) % 2 == 0; int l1 = 0, l2 = 0, r1 = len1 - 1, r2 = len2 - 1, piv1, piv2; int leftCt, rightCt; if (len1 == 0 && len2 == 0) { return 0; } else if (len1 == 0) { return (evenlen ? (nums2[r2/2] + nums2[r2/2+1]) / 2. : nums2[r2/2]); } else if (len2 == 0) { return (evenlen ? (nums1[r1/2] + nums1[r1/2+1]) / 2. : nums1[r1/2]); } // Reduce subsets until 1 or 2 medians remain while (true) { piv1 = l1 + (r1 - l1) / 2; piv2 = l2 + (r2 - l2) / 2; boolean nonZero1 = r1 - l1 >= 0, nonZero2 = r2 - l2 >= 0; int sz = (r1 - l1) + (r2 - l2); if (sz <= 2) { while (true) { leftCt = l1 + l2; rightCt = (len1 - 1 - r1) + (len2 - 1 - r2); if (evenlen && (r1 - l1) + (r2 - l2) == 0) { if (r1 - l1 == -1) return (nums2[l2] + nums2[r2]) / 2.; else if (r2 - l2 == -1) return (nums1[l1] + nums1[r1]) / 2.; else return (nums1[l1] + nums2[l2]) / 2.; } else if (!evenlen && (r1 - l1) + (r2 - l2) == -1) { if (r1 - l1 == -1) return nums2[l2]; else return nums1[l1]; } if (leftCt < rightCt) { // remove a smaller value if (r1 - l1 >= 0 && (r2 - l2 < 0 || nums1[l1] < nums2[l2])) l1++; else l2++; } else { // remove a larger value if (r1 - l1 >= 0 && (r2 - l2 < 0 || nums1[r1] > nums2[r2])) r1--; else r2--; } } } else { // General case leftCt = l1 + l2; rightCt = (len1 - 1 - r1) + (len2 - 1 - r2); if (leftCt > rightCt) { // remove from right // reduce array with max value on right if (!nonZero1 || !nonZero2) { // One array is empty if (nonZero1) r1 = piv1; else r2 = piv2; } else { if (piv1 < r1 && piv2 < r2) { // Both arrays have elements right of pivots if (nums1[piv1+1] > nums2[piv2+1]) r1 = piv1; else r2 = piv2; } else { if (piv1 == l1) { if (nums1[piv1] > nums2[piv2+1]) r1--; else r2 = piv2; } else { if (nums1[piv1+1] > nums2[piv2]) r1 = piv1; else r2--; } } } } else { // remove from left // reduce array with min value on left if (!nonZero1 || !nonZero2) { // One array is empty if (nonZero1) l1 = piv1; else l2 = piv2; } else { if (piv1 > l1 && piv2 > l2) { // Both arrays have elements left of pivots if (nums1[piv1-1] < nums2[piv2-1]) l1 = piv1; else l2 = piv2; } else { if (piv1 == l1) { if (nums1[piv1] < nums2[piv2-1]) l1++; else l2 = piv2; } else { if (nums1[piv1-1] < nums2[piv2]) l1 = piv1; else l2++; } } } } } } }

LeetCode (Algorithms#3) ‒ Longest Substring Without Repeating Characters

Problem

Given a string, find the length of the longest substring without repeating characters.

Examples:

Given "abcabcbb", the answer is "abc", which the length is 3.

Given "bbbbb", the answer is "b", with the length of 1.

Given "pwwkew", the answer is "wke", with the length of 3. Note that the answer must be a substring, "pwke" is a subsequence and not a substring.

Solution

The brute force approach entails looking at all O(n^2) substrings, and checking in O(n) if there are any repeated characters, resulting in O(n^3) time. The more efficient solution actually solves this in linear time. Through some simple bookeeping, we keep track of the starting position and length of the substring. While iterating through the string we must maintain the indices of repeated characters that were previously seen. A HashMap proves convenient, allowing for constant access to the index of each character. A simple int array could also be used at the cost of more space (for all possible characters).

At each character, we store the character's current index if it is either in the current max substring, or if it was previously, but is not anymore (Case 1). Otherwise, we have a character that is already in the current substring, in which case we offset the start of the substring to after the index of the first occurrence of the repeated character (and then save the new index). Below is the implementation of this algorithm. It is quite clean, and an important one to know as variations of it are very common as interview questions.

Time complexity: O(n)
Space complexity: O(n)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

public int lengthOfLongestSubstring(String s) { int max = 0, cur = 0, len = s.length(); Map<Character, Integer> m = new HashMap<Character, Integer>(); for (int i = 0; i < len; i++) { char c = s.charAt(i); Integer idx = m.get(c); if (!m.containsKey(c) || (idx != null && i - cur > idx)) { m.put(c,i); cur++; } else { cur = i - idx; m.put(c,i); } if (cur > max) { max = cur; } } return max; }

LeetCode (Algorithms#2) ‒Add Two Numbers

Problem

You are given two linked lists representing two non-negative numbers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.

Example:

Input: (2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 0 -> 8

Solution

The solution requires linear time and space, and is pretty straightforward. We perform simple addition as we were taught in elementary mathematics, starting with the smaller digits and carrying a 1 if necessary. The only trick is to do it in one loop which is easy because the digits are provided in reverse order. What if they weren't? Some backwards recursion could do the trick.

Time complexity: O(n)
Space complexity: O(n)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

public ListNode addTwoNumbers(ListNode l1, ListNode l2) { ListNode res = new ListNode(0); ListNode curs = res; ListNode cur1 = l1; ListNode cur2 = l2; int sum; boolean carry = false; while (true) { sum = (cur1 == null ? 0 : cur1.val) + (cur2 == null ? 0 : cur2.val) + (carry ? 1 : 0); carry = sum >= 10; curs.val = sum % 10; if ((cur1 == null || cur1.next == null) && (cur2 == null || cur2.next == null)) { if (carry) { curs.next = new ListNode(1); } break; } else { curs.next = new ListNode(0); curs = curs.next; cur1 = (cur1 == null ? null : cur1.next); cur2 = (cur2 == null ? null : cur2.next); } } return res; }

LeetCode (Algorithms#1) ‒ Two Sums

Problem

Given an array of integers, return indices of the two numbers such that they add up to a specific target.

You may assume that each input would have exactly one solution.

Example:

Given nums = [2, 7, 11, 15], target = 9,

Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

Solution

The brute force solution searches for the two indices in O(n^2) time. The problem can be solved in O(n) time and space using a hash table, where you simply look at each number x, and query the table for target - x.

Note: Use a HashMap to store indices as the values, with a unique integer hash function. The default function for Java's Integer is sufficient.

Time complexity: O(n)
Space complexity: O(n)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

public int[] twoSum(int[] nums, int target) { int[] res = null; Map<Integer,Integer> map = new HashMap<Integer,Integer>(nums.length); for (int i = 0; i < nums.length; i++) { map.put(nums[i], i); } for (int i = 0; i < nums.length; i++) { Integer j = map.get(target - nums[i]); if (j != null && i != j.intValue()) { res = new int[2]; res[0] = i; res[1] = j.intValue(); break; } } return res; }

Customizing Xcode: Plugins, Code Snippets, and more

When it come's to Apple development, your pretty much stuck with Xcode. As an IDE, it is comfortable, clean, and does a good job at encapsulating Apple's development environment. Although, like most Apple software, you sacrifice some freedom of control for a "better" user experience. Apple developers usually don't bother to configure Xcode beyond the default. And when using Xcode, it is not immediately evident that you have significant control over its look-and-feel, as well as the overall workflow.

For anyone that is remotely interested in improving their productivity with Xcode, I strongly recommend investing some time into configuring this IDE beyond the Apple comfort zone. Between plugins, code snippets, and keybinds, you can become significantly more efficient and comfortable with this IDE.

Note: As of Xcode 8, Apple has unfortunately removed support for plug-ins. The Plugins section was moved to the bottom of the post. We'll see what Apple does in the future as their decision to kill plugins has riled up many developers.

Code Snippets

Code snippets insert code using a shortcut that you define and select via Xcode's autocompletion. This is especially useful for a language like Objective-C which lacks conciseness. Within a snippet, code tags provide you with parameters that you can tab through to add code (e.g. <#code#>). This way, just a couple keystrokes can produce many commonly used lines of code, where you can then tab through to implement the specifics. It is important to not make your code snippets too specific or too general. You can also select the scope in which the code snippet is available, including: All, Class Implementation, Function or Method, String or Comment, etc. Code snippets are created in the Utilities panel of Xcode.

Ever encounter the absurd task of having to configure a scroll view to move content out from under the keyboard? This is a perfect situation for code snippets, which can generate these 140+ lines of code for you with just a few keystrokes. You will never again have to rumage through Apple Docs to dig out this lengthy solution to such a common problem.

Examples:

#pragma mark -
#pragma mark Table view data source

- (NSInteger)tableView:(UITableView *)tableView numberOfRowsInSection:(NSInteger)section {
    return <#num#>;
}

- (UITableViewCell *)tableView:(UITableView *)tableView cellForRowAtIndexPath:(NSIndexPath *)indexPath {
    UITableViewCell *cell = [tableView dequeueReusableCellWithIdentifier:<#(NSString *)#>];
    
    return cell;
}

#pragma mark -
#pragma mark Table view delegate

- (void)tableView:(UITableView *)tableView didSelectRowAtIndexPath:(NSIndexPath *)indexPath {
    <#code#>
}

Other useful snippets

Key Bindings

With Xcode you can configure key binds for any menu item, including those menu items added by plugins. These keybinds are especially useful with navigating Xcode since things can get a cluttered quite easily, especially when working on a Macbook. I recommend setting keybinds to show and hide the three common panels, as well as control the assistant editor. This allows for you to maximize viewing of the text editor, while keeping functionality within individual panels one keybind away. To accompany this method of navigating, the following default keybinds become exceedingly useful:

• cmd+shift+o to Quickly Open any file in the bundle (or methods, properties, and variables)
• enter (or click) to open in primary editor
  
• alt+enter (or click) to open in the assistant editor
  
• cmd+shift+up and down toggles between .h and .m files. (Adding alt toggles in the un-focused text editor)
• cmd+shift+left and right navigates back and forth between files in a text editor's history. (Adding alt toggles in the un-focused text editor)

(tabs are also available in Xcode with keybinds)

Plugins

One of the hidden capabilities of Xcode are plugins, of which there is little mention in any documentation. A few developers (like those at the Alcatraz.io team) have done great work to expose the plugin framework that Xcode is built on, and to make it easy to utilize for developers.

Plugins are built as bundles in Xcode where they have access to OS X features through libraries like AppKit and Foundation frameworks. These executables are stored in ~/Library/Application\ Support/Developer/Shared/Xcode/Plug-ins as plug-in bundles (.xcplugin extension) where they are loaded at startup of the IDE. The easiest way to manage these plugins is through Alcatraz, a package manager that maintains repositories of packages on github. Simply install Alcatraz, restart Xcode, and press Cmd+Shift+9 to browse and install packages.

Note that Xcode plugins rely on knowing the UUID of the current Xcode installation. If Xcode is updated, this UUID changes and some plugins may stop working. If this happens, you can simply reinstall the plugin, or follow this.

Here are some features that become available with plugins.

Code Formatting with BBUncrustifyPlugin

In my opinion, the most useful plugin, BBUncrustifyPlugin allows you to standardize your code formatting by specifying a ClangFormat or Uncrustify style, and configuring when formatting occurs (either when saving a file, or using a keybind). LLVM's webpage contains extensive documentation on clang-format here. See example below.

Example

.clang-format: (place this in your home directory where BBUncrustifyPlugin will look by default)

AllowAllParametersOfDeclarationOnNextLine: false
AllowShortBlocksOnASingleLine: false
AllowShortIfStatementsOnASingleLine: true
AllowShortLoopsOnASingleLine: true
AllowShortFunctionsOnASingleLine: false
AlignTrailingComments: true
AlignAfterOpenBracket: true
AlignTrailingComments: true
AlignConsecutiveAssignments: true
BinPackArguments: false
BinPackParameters: true
BreakBeforeBraces: Linux
ColumnLimit: 110
IndentWidth: 4
KeepEmptyLinesAtTheStartOfBlocks: false
ObjCSpaceAfterProperty: true
ObjCSpaceBeforeProtocolList: true
PointerBindsToType: false
SpacesBeforeTrailingComments: 1
TabWidth: 8
UseTab: Never

Customized Logging with XcodeColors + CocoaLumberjack

CocoaLumberjack is a simple logging framework that is optimized to give an order of magnitude increase in performance over NSLog. It offers individually configurable and dynamic log levels, as well as the ability to log to multiple outputs simultaneously. When combined with XcodeColors, you gain the capability of using colors in the Xcode debugging console. You can then create your own formatting for log messages at different levels.

Example

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76

@interface MGLogFormatter : NSObject <DDLogFormatter> @end @implementation MGLogFormatter - (NSString *)formatLogMessage:(DDLogMessage *)logMessage { NSString *logLevel; switch (logMessage->_flag) { case DDLogFlagError: logLevel = @"E"; break; case DDLogFlagWarning: logLevel = @"W"; break; case DDLogFlagInfo: logLevel = @"I"; break; case DDLogFlagDebug: logLevel = @"D"; break; default: logLevel = @"V"; break; } NSDateFormatter *df = [[NSDateFormatter alloc] init]; df.dateFormat = @"HH:MM:SS"; return [NSString stringWithFormat:@"%@ %@ <%@> %@", [df stringFromDate:logMessage->_timestamp], logMessage->_function, logLevel, logMessage->_message]; } @end @interface MGLogger : NSObject + (void)initLogger; @end @implementation MGLogger + (void)initLogger { // Enable XcodeColors setenv("XcodeColors", "YES", 0); // Standard lumberjack initialization [DDLog addLogger:[DDTTYLogger sharedInstance]]; // Add a custom formatter [DDTTYLogger sharedInstance].logFormatter = [[MGLogFormatter alloc] init]; // And then enable colors [[DDTTYLogger sharedInstance] setColorsEnabled:YES]; [[DDTTYLogger sharedInstance] setForegroundColor:DDMakeColor(100, 100, 100) backgroundColor:nil forFlag:DDLogFlagInfo]; [[DDTTYLogger sharedInstance] setForegroundColor:DDMakeColor(160, 160, 160) backgroundColor:nil forFlag:DDLogFlagDebug]; [[DDTTYLogger sharedInstance] setForegroundColor:DDMakeColor(254, 234, 88) backgroundColor:nil forFlag:DDLogFlagWarning]; [[DDTTYLogger sharedInstance] setForegroundColor:DDMakeColor(254, 81, 81) backgroundColor:nil forFlag:DDLogFlagError]; } @end

Themes

Beautify your Xcode editor with themes. These are nothing new to Xcode preferences, but Alcatraz makes obtaining color presets much easier. Simply install themes through the Package Manager, restart Xcode, and select them in preferences:

BladeRunner

eppz!

Vale

More themes here and in Alcatraz.

Extras

ColorSenseRainbow

Display colors within the editor when interacting with UIColor and NSColor objects.

KSImageNamed

Autocompletion of images in the project bundle for [UIImage imageNamed:].

SCXcodeSwitchExpander

Autocompletion of switch statements that generates cases for all enum values.

BBUDebuggerTuckAway

Auto-hide the Debugging Area upon typing.

DerivedData Exterminator

One-click removal of derived data for those times when you encounter some stubborn errors.

XToDo

Maintains a list of TODO comments (as well as FIXME, ???, !!!!)

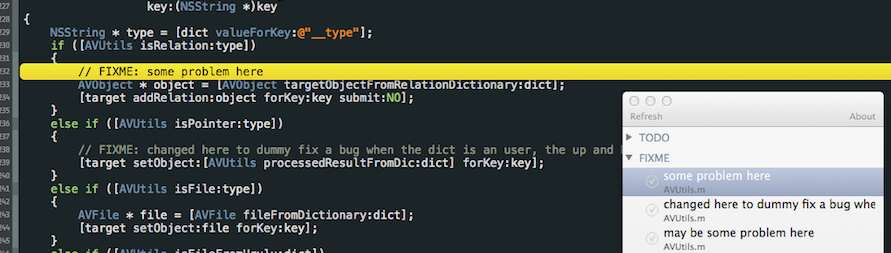
I hope this information is as useful to other Apple developers as it has been for me. Most other users of Xcode that I've worked with are not aware of these capabilities, and tend to be slightly stubborn when it comes to customizing it. All I can say is, it is not as difficult a task as it may seem and the payoff is great!